데이터분석과 관련하여 가장 중요한 것은 데이터가 어떻게 생겼는지 탐색하는 과정입니다.
이 과정에 데이터의 특정 변수의 분포를 관찰할 수도 있고, 서로 상관관계가 있는 변수들이 어떻것이 있는지 살표보는 과정이 있을 수도 있다. 하지만, 최근에는 데이터셋이 갖고 있는 변수의 숫자가 늘어남에 따라서 몇몇 특정 변수의 분포를 살펴보는 것으로 데이터를 탐색한다고 말하기가 어려운 상황입니다. 고차원의 데이터로부터 핵심적인 정보를 추려내고 시각화 한 후에야 데이터가 어떤 특징을 갖고 있는지 탐색하는게 가능합니다. 이러한 문제점을 해결해 줄 수 있는 방법으로 고차원 데이터의 차원을 줄여서 시각화 하는 기술은 매우 중요합니다. 이러한 기술로 주성분분석(Principle Component Analysis, PCA)와 t-Distributed Stochastic Neibhbor Embedding 방법이 있습니다. 본 블로그에서는 Python을 이용하여 PCA와 t-SNE를 이용하여 데이터의 차원을 줄이고, 시각화 하는 과정을 설명드리겠습니다.
MNIST dataset
MNIST-dataset은 데이터 분석 및 시각화 알고리즘을 테스트 하는데 많이 이용되고 있습니다. 이번 블로그에서도 MNIST 데이터를 사용하겠습니다.
import numpy as np
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata("MNIST original")
X = mnist.data / 255.0
y = mnist.target
print (X.shape, y.shape)이제 matrix와 vector 데이터를 Pandas DataFrame의 틀에 입력하겠습니다. Pandas DataFrame은 R에서 사용되는 데이터 구조와 비슷하기 때문에 R을 사용하는 유저라면, 추후에 비슷한 절차를 적용하여 데이터를 시각화 해 볼 수 있을 것입니다.
import pandas as pd
feat_cols = ['pixel'+str(i) for i in range(X.shape[1]) ]
df = pd.DataFrame(X,columns=feat_cols)
df['label'] = y
df['label'] = df['label'].apply(lambda i: str(i))
X, y = None, None
print( 'Size of the dataframe: {}'.format(df.shape) )전체 70,000 개의 숫자 데이터를 모두 이용하기에는 시간상의 제약이 있기 때문에, 무작위로 데이터를 추출하여 계산을 진행하겠습니다. 전체 70,000개의 데이터를 무작위로 순서를 섞은 후에 처음 5천개 또는 1만개 정도의 데이터를 계산 및 시각화에 이용하겠습니다.
rndperm = np.random.permutation(df.shape[0])
이제 계산 및 시각화에 사용할 무작위 데이터가 마련되었습니다. 계산에 사용하게될 데이터가 어떻게 생겼는지 임의로 30개의 데이터를 시각화 해보겠습니다.
import matplotlib.pyplot as plt
# Plot the graph
plt.gray()
fig = plt.figure( figsize=(16,7) )
for i in range(0,30):
ax = fig.add_subplot(3,10,i+1,title='Digit: ' + str(df.loc[rndperm[i], 'label']) )
ax.matshow(df.loc[rndperm[i], feat_cols].values.reshape((28,28)).astype(float))
plt.show()
시각화된 데이터를 살펴보니, 0에서부터 9까지의 필기체 숫자입니다. 필체가 조금씩 다르긴 하지만 0에서 9까지의 숫자들을 어떻게 구분할것인가? 는 고민해 볼 가치가 있는 일입니다. 이미 다양한 기계학습 알고리즘에서 이러한 숫자들을 99% 이상의 정확도로 구분하고 있긴 합니다만, 새로운 알고리즘들을 적용해 보기에 MNIST 데이터만큼 괜찮은 데이터셋도 없는것 같습니다.
MNIST 데이터셋의 숫자들은 28x28의 차원(즉, 784 차원)의 데이터라고 할 수 있습니다. 대체 기계학습 알고리즘은 데이터의 어떤 특징을 보고 숫자들을 구분해 내는 것일까요? 우선 PCA를 통해서 784 차원의 데이터를 2차원의 데이터로 축소해 보겠습니다.
Dimensionality reduction using PCA
PCA는 데이터에 있는 정보들를 대부분 유지하면서 차원을 줄이는 통계방법입니다. 우리 인간은 3차원이 넘어가는 데이터로부터 시각적으로 유용한 정보를 찾기가 굉장히 어렵습니다. PCA를 이용하여 784 차원의 데이터를 3차원으로 줄이고, 이것을 시각화해 보면, 각 숫자(0~9) 마다 어떤 특징이 있는지 알아보기가 쉬워집니다.
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca_result = pca.fit_transform(df[feat_cols].values)
df['pca-one'] = pca_result[:,0]
df['pca-two'] = pca_result[:,1]
df['pca-three'] = pca_result[:,2]
print( 'Explained variation per principle component: {}'.format(pca.explained_variance_ratio_))PCA 분석 결과 처음 두개의 성분이 데이터의 17% 정도를 설명한다고 나옵니다. 원글에서는 처음 두개의 PCA 성분이 데이터의 25%를 설명한다고 나오는데, replication하는 과정에서 실수가 있었는지... 어느 부분이 잘못되었는지는 모르겠지만, python3에서 분석을 진행했을때는 값이 조금 다르게 나오는것 같습니다. 여튼 variance가 가장 큰 것부터 처음 2개의 principle component를 그려보면 아래 그림과 같은 결과를 얻을 수 있습니다.
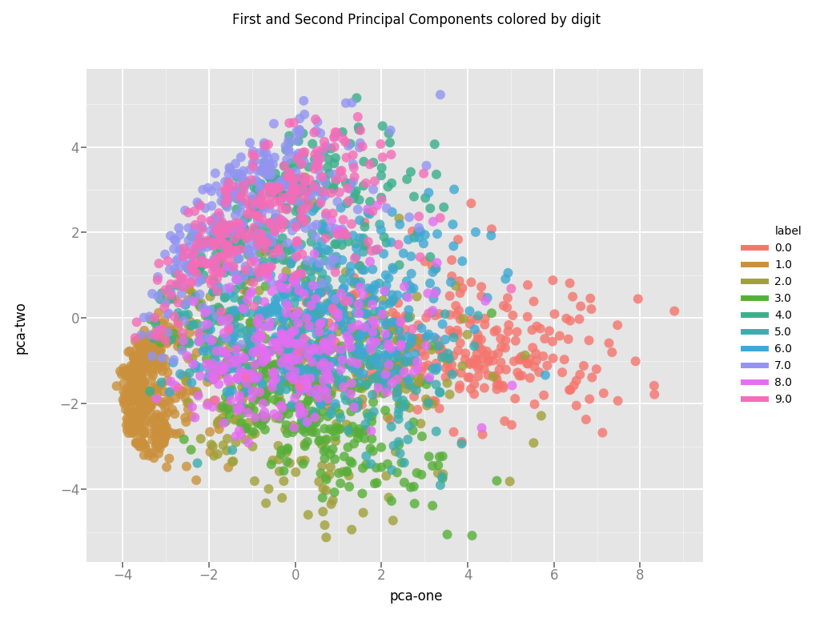
그림에서는 숫자0과 숫자1은 어느정도 PCA 성분의 차이가 보이지만, 그 밖에 숫자들은 거의 구분이 되지 않습니다. 다행스럽게도 이런 경우에 적용해 볼 수 있는 다른 방법이 있는데, 바로 t-SNE (t-Distributed Stochastic Neighboring Embedding) 입니다.
T-Distributed Stochastic Neighboring Embedding (t-SNE)
t-SNE는 데이터 차원을 축소하는데 사용되는 기법입니다. 특히, 고차원의 데이터를 시각화 하는데 아주 유용하게 사용되는 방법입니다. t-SNE 알고리즘에 대한 자세한 설명은 링크되어 있는 논문을 통해서 공부해 보시기 바랍니다.
t-SNE는 원본 데이터를 가장 잘 표현할 수 있도록 데이터의 차원을 줄이는 방법입니다. t-SNE 알고리즘은 많은 계산이 요구되기 때문에, 1차적으로 차원을 축소한 후에 t-SNE 알고리즘에 데이터를 입력해야 하는 경우도 있을 것입니다. 또한, t-SNE 알고리즘은 N개의 데이터가 있을때 N^2 만큼 시간이 오래걸리기 때문에 실제 데이터를 분석하는데 있어서 제한적일 수 있습니다.
It is highly recommended to use another dimensionality reduction method (e.g., PCA for dense data or TruncatedSVD for sparse data) to reduce the number of dimensions to a reasonable amount (e.g. 50) if the number of features is very high.
위에서 언급한 한계를 기억하며, sklearn 라이브러리를 이용하여 알고리즘을 작성해 보겠습니다. MNIST 데이터는 데이터의 차원이 크지는 않지만 데이터가 70,000개 정도 있기 때문에 분석에 사용되는 데이터를 전체의 약 10% 정도인 7,000개로 줄여서 분석을 진행해 보겠습니다.
import time
from sklearn.manifold import TSNE
n_sne = 7000
time_start = time.time()
tsne = TSNE(n_components=2, verbose=1, perplexity=40, n_iter=300)
tsne_results = tsne.fit_transform(df.loc[rndperm[:n_sne],feat_cols].values)
print( 't-SNE done! Time elapsed: {} seconds'.format(time.time() - time_start )이제 t-SNE를 이용한 차원축소 결과를 얻었고, 시각화하는 과정만 남았습니다. ggplot을 이용하여 2차원 평면상에 주요한 2개의 값을 그래프로 그리면서, 각 숫자별로 다른 색으로 시각화를 하면, t-SNE가 데이터의 특징을 얼마나 잘 추려내면서 차원 축소를 했는지 확인해 볼 수 있을 것입니다.
df_tsne = df.loc[rndperm[:n_sne],:].copy()
df_tsne['x-tsne'] = tsne_results[:,0]
df_tsne['y-tsne'] = tsne_results[:,1]
chart = ggplot( df_tsne, aes(x='x-tsne', y='y-tsne', color='label') ) \
+ geom_point(size=70,alpha=0.1) \
+ ggtitle("tSNE dimensions colored by digit")
chart
시각화 결과를 보면 (PCA에 비해) 각 숫자들을 아주 잘 구분해 주는 것을 알 수 있다. 만약 분석에 사용되는 데이터 샘플의 숫자를 줄이지 않고, t-SNE를 이용하고 싶다면, PCA를 이용해서 원본 데이터를 50차원 정도로 줄인 후에 t-SNE를 적용하는 방법을 추천한다.
이 글은 Luuk Derksen의 원글을 듬성듬성 번역 했음을 밝히며, 번역자 맘대로 해석된 부분이 많이 있습니다. 원글은 아래 링크에서 볼 수 있습니다.
https://medium.com/@luckylwk/visualising-high-dimensional-datasets-using-pca-and-t-sne-in-python-8ef87e7915b
'데이터과학 > 데이터 분석 실습' 카테고리의 다른 글
| OBV 거래량 지표를 이용한 알고리즘 투자 전략 (feat. 파이썬) (1) | 2020.12.25 |
|---|---|
| 이동평균선과 RSI를 이용한 알고리즘 투자전략 (feat. 파이썬) (1) | 2020.12.25 |
| 뇌영상 데이터 분석 - Create Brain Mask (1) | 2015.07.10 |
| 뇌영상 데이터 분석 - Matlab Index scheme (0) | 2015.06.25 |
| intuitive voxel-based lesion symptom mapping (iVLSM) toolbox (0) | 2015.04.15 |



