앞서 시계열 데이터 분석 및 예측을 위한 완벽 가이드에서 시계열 데이터 분석에 있어 데이터의 안정성(Stationary)을 확인하는 것이 중요함을 소개해 드렸습니다. 이번에는 파이썬으로 ADF (Augmented Dickey-Fuller) 테스트와 KPSS (Kwiatkowski–Phillips–Schmidt–Shin) 테스트를 수행하는 방법에 대해서 설명해 드리겠습니다.
라이브러리 Import
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')시계열 데이터는 야후 파이낸스에서 가져오겠습니다. 만약 yfinance 라이브러리가 설치가 안되었다면, 아래의 명령어를 통해서 설치해 주세요.
!pip install yfinance주식 데이터 로드
import yfinance as yf
# 테슬라
df_tsla = yf.download('TSLA', start="2019-12-01", end="2020-11-30")
# LG화학
df_lg = yf.download('051910.KS', start="2018-12-01", end="2020-11-30")
# 리튬아메키라
df_lac = yf.download('LAC', start="2018-12-01", end="2020-11-30")
# 각 종목의 종가 데이터만 모아서 하나의 테이블로 합치기
df = pd.merge(df_tsla['Adj Close'], df_lg['Adj Close'], left_index=True, right_index=True, how='left').rename(columns = {'Adj Close_x':'TSLA', 'Adj Close_y':'LG'})
df = pd.merge(df, df_lac['Adj Close'], left_index=True, right_index=True, how='left').rename(columns = {'Adj Close':'LAC'})
df.dropna(inplace=True)
df.head()
시계열 데이터 시각화
# 예시로 LG화학 주가 데이터 시각화
columns = ['LG_Chem']
df[columns].plot(figsize=(12.2,6.4)) #Plot the data
ADF 안정성 테스트
ADF 테스트는 시계열이 안정적(Stationary)인지 여부를 확인하는데 이용되는 방법입니다.
- Null hypothesis: 기각에 실패하면 시계열이 안정적이지 않음을 의미합니다.
- Alternative hypothesis: 귀무 가설(null hypothesis)이 기각되고 시계열이 안정적임을 의미합니다.
n_obs = 20
df_train, df_test = df[0:-n_obs], df[-n_obs:]
from statsmodels.tsa.stattools import adfuller
def adf_test(df):
result = adfuller(df.values)
print('ADF Statistics: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
print('ADF Test: Tesla time series')
adf_test(df_train['TSLA'])
print('ADF Test: Lithium Americas time series')
adf_test(df_train['LAC'])
print('ADF Test: LG Chem time series')
adf_test(df_train['LG_Chem'])
p-value>0.05 이므로 귀무 가설을 기각 할 수 없습니다. 따라서 세 개의 시계열은 안정적이지 않습니다.
KPSS 안정성 테스트
KPSS 검정은 시계열이 평균 또는 선형 추세 주변에 고정되어 있는지 또는 단위 루트(unit root)로 인해 고정되지 않은지 확인합니다.
- Null hypothesis: 시계열이 안정적입니다.
- Alternative hypothesis: 시계열이 안정적이지 않습니다.
from statsmodels.tsa.stattools import kpss
def kpss_test(df):
statistic, p_value, n_lags, critical_values = kpss(df.values)
print(f'KPSS Statistic: {statistic}')
print(f'p-value: {p_value}')
print(f'num lags: {n_lags}')
print('Critial Values:')
for key, value in critical_values.items():
print(f' {key} : {value}')
print('KPSS Test: Tesla time series')
kpss_test(df_train['TSLA'])
print('KPSS Test: Lithium Americas time series')
kpss_test(df_train['LAC'])
print('KPSS Test: LG Chem time series')
kpss_test(df_train['LG_Chem'])
p-value<0.05 이므로 귀무 가설을 기각하며 세 개의 시계열은 안정적이지 않음을 알 수 있습니다.
ADF 테스트와 KPSS 테스트를 모두 사용하여 시계열의 안정성에 대해 교차 확인합니다. 여기에 있는 세 개의 시계열 데이터가 안정적이지 않다는 결론을 내릴 수 있습니다. 차분(또는 비율)으로 시계열을 변환하여 안정적으로 만들 수 있습니다.
일일 수익률(=변화율)로 변환하기
- 시계열을 안정적으로 만들기 위해서는 두개의 연속된 시계열 값의 차분(difference)을 취하는 방법이 가장 많이 사용되는 방법입니다.
- 하지만 주식 시계열 데이터에서는 차분 값보다는 수익률이 더욱 이해가 쉽기 때문에 일일 변화화을 계산하여 시계열 데이터를 안정화하는 방법을 추천합니다.
# 일일 주가 변화율 계산
for col in df.columns:
df['r_'+col] = 100*df[col].pct_change()
df.dropna(inplace=True)
df.head()
일일 수익률(=주가 변화율) 시각화 하기
columns = ['r_TSLA']
df[columns].plot(figsize=(12.2,6.4)) #Plot the data
변화율에 대해서 ADF 테스트를 다시 수행
n_obs = 20
df_train, df_test = df[0:-n_obs], df[-n_obs:]
print('ADF Test: Tesla time series')
adf_test(df_train['r_TSLA'])
print('ADF Test: Lithium Americas time series')
adf_test(df_train['r_LAC'])
print('ADF Test: LG Chem time series')
adf_test(df_train['r_LG_Chem'])
변화율에 대해서 ADF 테스트를 진행하니 p-value가 0.05 수준보다 훨씬 낮으므로 귀무 가설을 기각합니다. 따라서 현재 변화율 데이터는 안정적이라고 할 수 있습니다.
변화율에 대해서 KPSS 테스트를 다시 수행
print('KPSS Test: Tesla time series')
kpss_test(df_train['r_TSLA'])
print('KPSS Test: Lithium Americas time series')
kpss_test(df_train['r_LAC'])
print('KPSS Test: LG Chem time series')
kpss_test(df_train['r_LG_Chem'])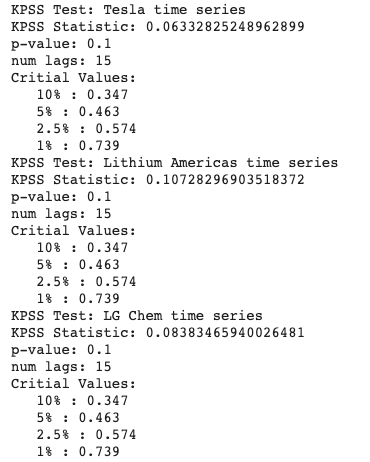
변화율에 대한 KPSS 테스트에서는 세 개의 시계열 모두 p-value가 0.05보다 큰 값을 가지므로 귀무 가설을 기각할 수 없으며 안정적이라고 할 수 있습니다.
지금 까지 시계열 데이터의 안정성을 확인하는 두가지 방법에 대해서 예제와 함께 설명 드렸습니다. 보통 주가 데이터(특히 나스닥 상장 기술주의 시계열 데이터)는 우상향 하는 경향이 있습니다. 이렇게 시계열에 경향성(trend)이 있으면 안정적이지 않습니다. 데이터를 분석하기 전에 안정성 테스를 꼭 해보시기 바랍니다.
'데이터과학 > 데이터 분석 실습' 카테고리의 다른 글
| 실제 강도 지수를 이용한 알고리즘 트레이딩 (feat. 파이썬) (1) | 2020.12.31 |
|---|---|
| 스토캐스틱 지표를 이용한 알고리즘 투자전략 (feat. 파이썬) (0) | 2020.12.30 |
| 금융 포트폴리오 최적화 (feat. 파이썬) (7) | 2020.12.25 |
| 자금 흐름 지표를 이용한 알고리즘 투자 전략 (feat. 파이썬) (0) | 2020.12.25 |
| OBV 거래량 지표를 이용한 알고리즘 투자 전략 (feat. 파이썬) (1) | 2020.12.25 |



